论文: He K, Zhang X, Ren S, et al. Deep Residual Learning for Image Recognition[J]. Computer Science, 2015.
Github: https://github.com/KaimingHe/deep-residual-networks
译文推荐:http://www.cnfeelings.com/future/53100 论文:Ioffe S, Szegedy C. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift[J]. Computer Science, 2015.
部分内容摘自:
http://blog.csdn.net/happynear/article/details/44238541 作者:happynear
http://blog.csdn.net/hjimce/article/details/50866313 作者:hjimce
http://blog.csdn.net/shuzfan/article/details/50723877 作者:shuzfan
BN的matlab代码:https://github.com/happynear/DeepLearnToolbox
Caffe的BN实现:https://github.com/ducha-aiki/caffe/tree/bn
论文算法概述
训练深度神经网络时,每层网络的输入分布都会随着前面层的参数变化而改变。所以需要较低的学习率和谨慎的参数初始化,这会使训练变得缓慢,使saturating nonlinearities 激活函数(如sigmoid,正负两边都会饱和)进行模型训练也会变得困难。文中称这种现象为internal covariate shift,并采用归一化网络层的输入(Batch Normalization)来解决该问题。
“We define Internal Covariate Shift as the change in the distribution of network activations due to the change in network parameters during training”
-
Batch Normalization可以保持各层输入的均值和方差稳定,来减弱internal covariate shift问题,并提高训练速度。
-
可以通过降低梯度对于参数的尺度或初始值的依赖性,对整个网络的梯度流起到有利的效果,这可以使我们可以使用更高的学习率而没有发散的风险。
-
有正则化效果,规范化了模型,减少了Dropout的需求。
-
降低网络在饱和区域卡死的可能性降低,使网络使用saturating nonlinearities 激活函数成为可能。
网络训练的预处理
从以往的论文可得如果输入数据是白化的(0均值、1方差、弱相关),则网络的收敛速度会快些。而每层网络的输入都由前面层产生,这有利于实现对每层的输入进行相同的白化,白化后有助于固定输入的分布,来去除internal covariate shift的缺点。
如图中红点,由于图像数据的每一维一般都是0-255之间的数字,因此数据点只会落在第一象限,而且图像数据具有很强的相关性,比如第一个灰度值为30,比较黑,那它旁边的一个像素值一般不会超过100,否则给人的感觉就像噪声一样。由于强相关性,数据点仅会落在第一象限的很小的区域中,形成类似上图所示的狭长分布。而神经网络模型在初始化的时候,权重W是随机采样生成的,一个常见的神经元表示为:ReLU(Wx+b) = max(Wx+b,0),即在Wx+b=0的两侧,对数据采用不同的操作方法。具体到ReLU就是一侧收缩,一侧保持不变。
在使用梯度下降时,可能需要很多次迭代才会使这些虚线对数据点进行有效的分割,就像紫色虚线那样,这势必会带来求解速率变慢的问题。更何况,我们这只是个二维的演示,数据占据四个象限中的一个,如果是几百、几千、上万维呢?而且数据在第一象限中也只是占了很小的一部分区域而已,可想而知不对数据进行预处理带来了多少运算资源的浪费,而且大量的数据外分割面在迭代时很可能会在刚进入数据中时就遇到了一个局部最优,导致overfit的问题。这时,如果我们将数据减去其均值,数据点就不再只分布在第一象限,这时一个随机分界面落入数据分布的概率增加了多少呢?2^n倍!如果我们使用去除相关性的算法,例如PCA和ZCA白化,数据不再是一个狭长的分布,随机分界面有效的概率就又大大增加了。不过计算协方差矩阵的特征值太耗时也太耗空间,我们一般最多只用到z-score处理,即每一维度减去自身均值,再除以自身标准差,这样能使数据点在每维上具有相似的宽度,可以起到一定的增大数据分布范围,进而使更多随机分界面有意义的作用。

通过Mini-Batch统计进行归一化
如果对每一层都进行PCA白化,计算量过大,因此作者只采用了减均值除标准差的方式对每个标量特征进行归一化,这样可以加快网络的收敛,尽管这些特征并非弱相关。
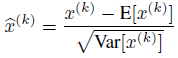
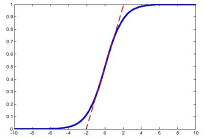
但如果对每层都进行这种简单的归一化会影响层的表达能力。比如下图,在使用sigmoid激活函数的时候,如果把数据限制到0均值单位方差,那么相当于只使用了激活函数中近似线性的部分,这显然会降低模型表达能力。为此,作者添加了两个参数对归一化量进行缩放和偏移。
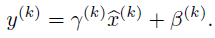
其中均值E和方差Var,在理想情况下应是针对整个数据集的,但显然这是不现实的。因此,作者做了简化,用一个Batch的均值和方差作为对整个数据集均值和方差的估计。BN算法整体如下:

在训练时,需要将loss L的梯度通过该变换进行反向传播,推导过程采用链式法则,公式如下:
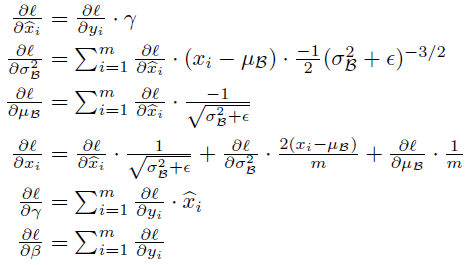
在测试时, 均值和方差已经不是针对某一个Batch了,而是针对整个数据集。因此,在训练过程中除了正常的前向传播和反向求导之外,还要记录每一个Batch的均值和方差,以便训练完成之后按照下式计算整体的均值和方差:
实验结果

