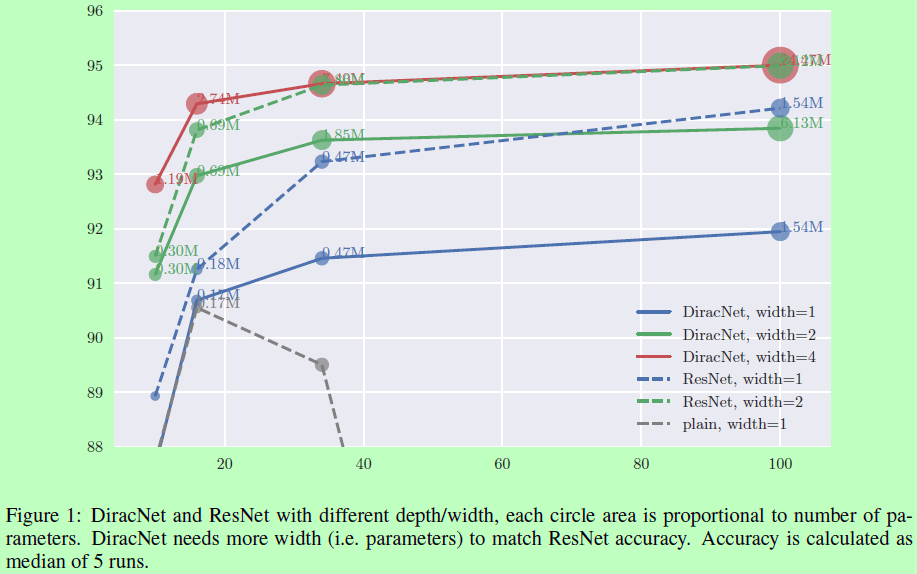
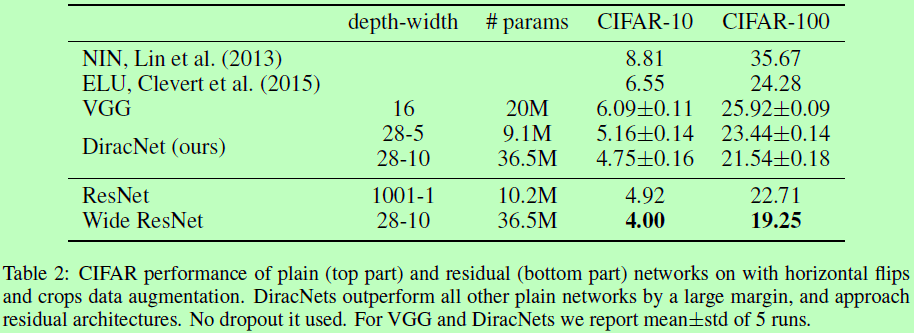
论文： Zagoruyko S, Komodakis N. DiracNets: Training Very Deep Neural Networks Without Skip-Connections[J]. 2017.
Github: https://github.com/szagoruyko/diracnets
论文算法概述
带有skip-connections的深度神经网络，如ResNet，其性能很好。但skip-connections有以下问题：1、特征重用问题：前一层特征图输入更高层时，无法保证都能学习到有用的特征表示；2、网络加宽比加深对性能的提升更为有效；3、实际的深度不明确：这深度可能是由网络里的最短路径来决定的。
出于这些考虑，作者提出了一种Dirac权重参数化方法，使我们能够训练很深的plain结构的网络，而不需要使用到skip-connections就能达到同样的性能。而且Dirac-parameterized滤波器可以被看成一个单一的向量，这样网络就如VGG那样简单且容易分析。Dirac parameterization也可以在ResNet上使用，实验证明可以消除ResNet不能随便初始化的问题。
Dirac parameterization
受ResNet的启发，将参数化权重作为Dirac函数的残差，而不再使用skip connection。将任何输入与Dirac进行卷积会得到相同的输入，即定义为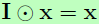
，这样有助于将信息传播到网络更深的地方，类似的在反向传播中也有助于缓解梯度弥散问题。因为卷积可以看成是矩阵相乘，所以I为一个简单的单位矩阵。将这个运算推广到卷积层中，令输入为
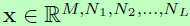（内含M个通道，分别为N1…NL），与含M个滤波器的权重
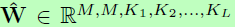卷积，生成M个通道的输出
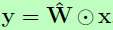。这样，定义Dirac delta为
基于上面的定义，对于忽略偏置项的卷积层y，令a为训练时的缩放向量，W为权重时，其权重的参数化公式为：
a的第i个元素都对应着W中的第i个滤波器的缩放，当a的所有元素都接近0时，就变回了原始的卷积层。
作者也进一步尝试了对W进行欧几里德范式归一化Wnorm，再加一个缩放向量b，则有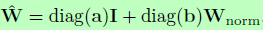
Experiments
