论文: Zhang T, Qi G J, Xiao B, et al. Interleaved Group Convolutions for Deep Neural Networks[J]. 2017.
论文算法概述
提出一种基于分组卷积group convolution设计的IGC(Interleaved Group Convolutions)网络结构,是一种将输入通道分成多个部分,然后再分别在各个通道上单独做常规卷积的方法。一个分组卷积可以看成是一个带有稀疏的block-diagonal形式的卷积核的常规卷积,而每个block对应着一个以通道划分的部件partition,每个部件之间没有任何联系。IGC包含有两组卷积,以primary group convolution和secondary group convolution表示, primary分组卷积用于处理空间相关性,采用3x3卷积核,单独分别对每个部件的通道进行处理。使用secondary分组卷积去融合由primary分组输出的各个部件的通道,采用1x1卷积核。
IGC在参数数量和计算时间复杂度不变的情况下,IGC比常规的卷积更宽。每个IGC的block包含有两组卷积。结构如下图1所示:
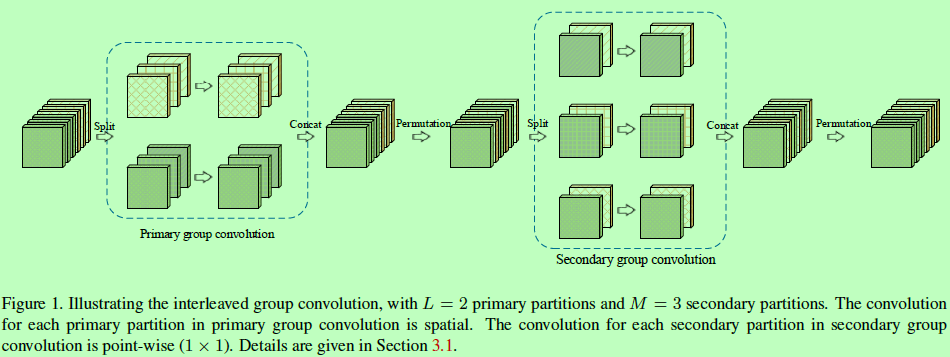
Primary group convolutions
令L为部件数量,称为primary partitions,让每个部件包含相同的通道数M。primary分组卷积在单一空间位置上,定义如下:

Secondary group convolutions
将由primary分组卷积输出的通道{y1,y2,…yL}交换到M个secondary部件中,其中每个部件包含有L个通道,即在一个secondary部件内含有的通道是来自不同primary部件,第m个secondary部件由每个primary部件的第m个输出通道组成。具体定义如下:

Primary + Secondary
总之,一个IGC模块可以定义如下,意味着其等价于一个常规卷积,而其卷积核由两个稀疏矩阵相乘得到。

Analysis:Wider than regular convolutions
在primary分组卷积中核大小为S,secondary中的为1(=1x1)。以单一空间位置为例,IGC的参数数量(在特征图大小固定时,参数数量等同于计算复杂度)为T_igc=(L x M x M x S + M x L x L) = G x G x (S/L + 1/M)。其中G=ML就是IGC的宽度(即通道数量)。而对于带有相同大小卷积核S的常规卷积,在其输入输出宽度(通道数)为C时,参数数量T_rc=C x C x S。
令参数数量相同,T_igc=T_rc=T,则有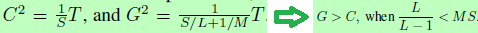 。因此当L大于1时,IGC就会比常规卷积宽。
。因此当L大于1时,IGC就会比常规卷积宽。
Analysis:When is the widest?

Analysis:Wider leads to better performance?
参考以上公式5,固定参数大小,即可由以下约束
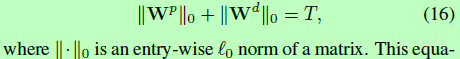
该公式表示当IGC更宽或输入维度更大时,两个W都会更大,但同时也会更稀疏。即合成的卷积核越大,其受到的约束就会更多,在这约束的影响下宽度并不是越宽越好。在作者的两个实验中M=2时能取得最佳效果。

Experiments
实验的结构搭配是IGC+BN+ReLU。