论文： Liu W, Wen Y, Yu Z, et al. SphereFace: Deep Hypersphere Embedding for Face Recognition[J]. 2017.
论文算法概述
该论文主要是提出了A-Softmax loss用于CNN去学习具有识别能力的人脸特征。
Introducing Angular Margin to Softmax Loss
作者主要提出了一种学习angular margin的方法。从softmax loss的分析中可以知道，决策边界在很大程度上决定了特征分布，因此作者的主要思路是操纵决策面去生成angular margin。下面以二分类为例去诠释这个idea。
假设给定一个从class 1中训练得到的特征x，以及x与W_i之间的角度theta_i。因为二分类中softmax公式如下：
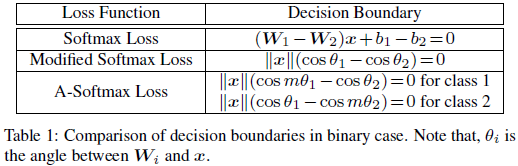
要x准确分类为class 1，则需p1>p2，即需要W1^T x + b1 > W2^T x + b2，则决策边界为(W1-W2) x + b1 - b2 = 0，其中由点积公式a . b=\a\ \b\ · cos(theta)得: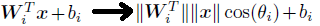
.
为简化，归一化权重去掉偏置，即使令\Wi=1，bi=0，则当cos(theta1)>cos(theta2)时，x才被正确分类。但如果用cos(m x theta1)>cos(theta2)来代替（其中m>=2，整数），这本质上会使决策变得更严格，因为需要cos(theta1)的更低的界限仍比cos(theta2)高。则类别1的决策线为cos(m x theta1)=cos(theta2)。类似的，如果需要cos(m x theta2)>cos(theta1)来使特征正确分类到class2，则class2的决策线为cos(m x theta2)=cos(theta1)。假设所有训练样本都能被正确分类，则这决策面会生成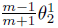
的一个angular margin.其中theta12是W1与W2间的角度。从角度的观点看，将x正确分类到class1需要theta1<theta2/m，而把x正确分类到class2需要theta2<theta1/m，比原先的theta1<theta2和theta2<theta1的要求更严格。则有以下修改后的softmax公式：
其中theta yi;i的取值范围是[0,pi/m]，为了去掉这个限制，令其可在CNN上进行优化，作者将cos(theta yi;i)的范围进行扩展，方法是通过归纳其到一个单调递减的函数Psi(theta yi;i)，这个函数应与cos(theta yi;i)在[0,pi/m]等价。因此，作者提出的A-Softmax loss公式如下：
其中Psi(theta yi;i)定义为:
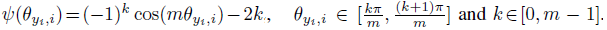
| m>=1，为整数，控制着angular margin的大小，当m=1时，它变成了普通的modified softmax loss（即 | W | =1，b=0）。 |
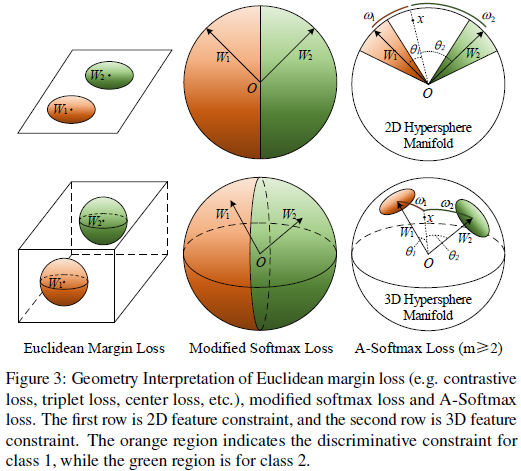
A-Softmax loss对各个不同的类采用不同的决策边界（每个决策边界会比原来的更严格），因此而产生angular margin。从原始的softmax loss到modified softmax loss，即从优化内积到优化角度。而从modified softmax loss到A-Softmax loss，即将决策边界变得更严格和更分离。这angular margin随m的增大而增大，而m=1时其为0。
以A-Softmax loss作为监督信号，CNN以几何角度解释的angular margin来学习人脸特征。因为A-Softmax需要Wi=1，bi=0，这使预测只取决于样本x和Wi之间的角度。因此x可以以最小的角度被正确分类。参数m的意义在于学习不同类别之间的angular margin。为便于角度计算和反向传播，作者以一个只包含有W和xi的表达式来将cos(theta j,i)和cos(mtheta yi;i)，这个表达式很容易用cosine和多个角度公式来实现定义（这也是为什么要求m为整数的原因）。没有了theta，则可以计算x和W的导数，与softmax loss类似。
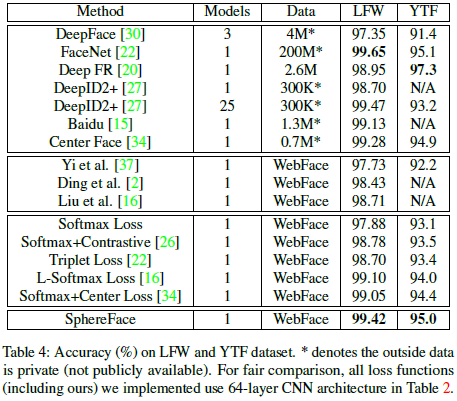
Experiments
