ChenJM
NormFace（2017）

  21 May 2017

论文： Wang F, Xiang X, Cheng J, et al. NormFace: L2 Hypersphere Embedding for Face Verification[J]. 2017.

Github: https://github.com/happynear/NormFace

论文算法概述

   在典型的人脸验证任务中，特征归一化是提升性能的关键一步。论文中提出了基于归一化特征的两个策略用于训练。第一个是修改过的softmax loss，优化了余弦相似度，代替了内积操作。第二是通过为每一类引入一个agent vector来重新定义训练度量标准。这两个策略能使模型在LFW上提升0.2到0.4的准确率。

   该论文中提出和解释了四个问题：

  1. 对于通过分类loss（特别是softmax loss）训练得到的特征，在做特征比对的时候，为什么特征归一化会变得高效？

  2. 为什么使用softmax loss直接去优化余弦相似度会导致网络无法收敛？

  3. 在使用softmax loss时，如何去优化余弦相似度？

  4. 使用softmax loss的模型在做特征归一化后无法收敛，那么有没有其他loss函数适合做归一化？

Necessity of Normalization

为直观了解softmax loss，在mnist数据集上训练了一个lenet模型作为例子。先将特征维降低到2，并画了10w个训练样本的2维特征在平面上，如图2所示。从图中可以看到，如果使用欧式距离作为度量方式，则f2与f1之间的距离比f2到f3的近很多，达不到好的效果。而同时可以看到，对于这些特征以角度进行划分的效果会比欧式距离和内积要好，所以之前很多都会采用余弦相似度作为度量方法，尽管训练的时候用的是softmax loss。而softmax loss是非归一化特征的内积运算，因此训练的度量方法和测试用的度量方法一定的分歧。

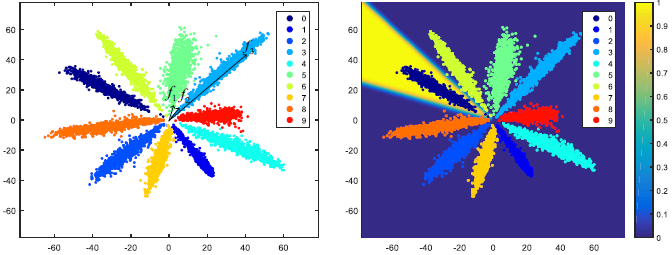
为什么softmax loss会趋向取产生这样“呈放射状”的特征分布呢？原因是softmax loss实际上表现为soft version of max operator。对特征向量的量级进行缩放不会影响到它们的类别结果，回顾softmax loss的公式定义如下：

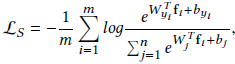
其中m是训练样本数量，n是类别数量，fi是第i个样本的特征，yi是对应的标签（范围是[1,n]），W和b分别是softmax loss之前的最后一个内积层的权重矩阵和偏置向量，Wj是W的第j列，对应着第j类别，在测试的阶段，通过下式进行分类：

这里先假定(Wi x f + bi) - (Wj x f + bj) >= 0，再假定去掉偏置项b，则以表示x被分类到类别i的概率。对于任意给定的尺度s>1，若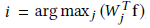，那么Pi ( sf ) >= Pi ( f )会恒成立。（推导过程看论文附录7.1）。这意味着softmax loss会趋向于使区分能力强的特征具有更大的量级，也是为什么softmax的特征分布会呈放射状的原因。然而我们并不需要这种特性。通过归一化，能够消除这个影响。因此，通常会采用余弦来度量两个向量的相似度。

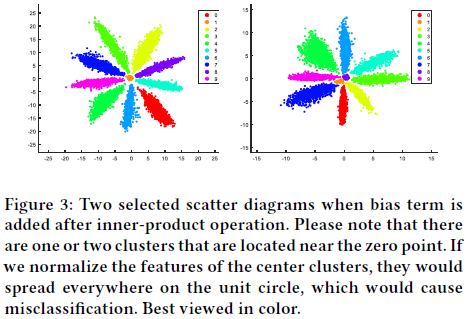
然而，上面的讨论是基于在内积后没有添加偏置项目的情况的，实际上，就算两个类别的权重向量在一样的时候，模型依然能通过偏置项来进行决策。如图3可以发现某与某些类的一些点落到了原点附近，而归一化后来这些自各类的点可能会散布开在一个圆内，与其他的类别相重叠，破坏其特征的可区分能力。为了避免这种风险，论文中在softmax loss之前不添加偏置项！

Layer Definition

对于输入向量x，L2归一化层的输出的归一化向量为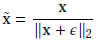，其中分母第二项为一个小的正数以防止分母为0，x可以是特征向量f或权重矩阵Wi中的一列。在反响传播时，梯度w.r.t可以通过链式法则获得：

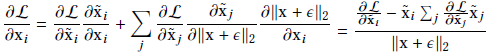
而x与rho L / rho x是相互正交的，从几何角度上看，梯度rho L / rho x是rho L / rho ~x是在向量~x的单元超球面上的切线空间上的映射，从下图4所示。图4左可以推导出，更新后   x   2通常会增加，为了防止   x   2无限增长，对应向量x有必要采用权重衰减的策略。

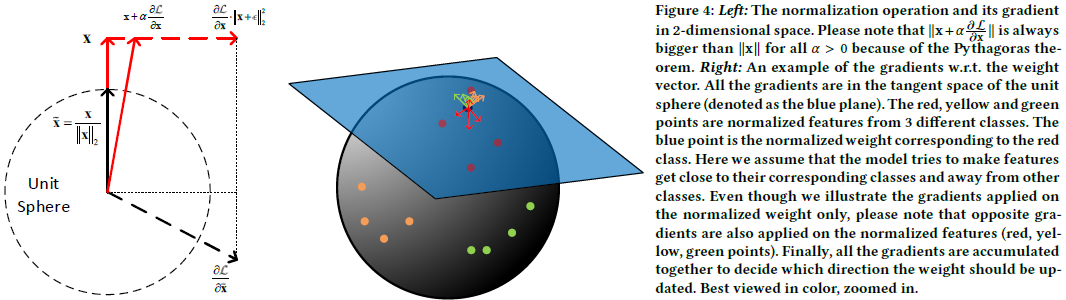
Reformulating Softmax Loss

使用归一化层，可以直接优化余弦相似度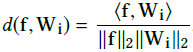，其中f为特征，Wi表示softmax loss层之前的内积层上权重矩阵的第i列。然而，在归一化后，网络无法收敛，loss下降缓慢，在几千次迭代后收敛到一个很大的值。这主要原因是在归一化后d( f,Wi )的范围是[-1,1]，在使用内积层和softmax层，它通常会分布在（-20，20）和（-80，80）。这样的low range问题，在yi对应的就是f的标签且样本能够很好的被区分开来的情况下，也可能会阻碍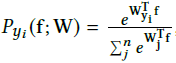接近1。举个极端的例子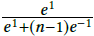，的值很小（n=10时为0.45；n=1000时为0.007），远离1，而在这种条件下，所有其他类的样本都在单元超球面的另外一边，可以很好地被区分开来。模型通常会尝试给容易分类的样本一个大的梯度，这样困难样本可能无法获得足够的梯度信息。

为了解释这个问题，提出(Softmax Loss Bound After Normalization)的命题。假设每类都有相同数量的样本，且所有样本都很容易被区分（如每个样本的特征都与其对应类别的权重一致）。如果我们将特征和权重矩阵的每列都进行归一化，则softmax loss将会有一个更低的限制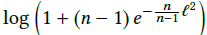，，其中n为类别数量。（推导过程看论文附录7.2）。这个限制意味着如过我们只将特征和权重归一化到1，那么softmax loss在训练样本中将会被限制到一个很大的值，尽管没有使用正则化。举个真实的例子，如果在CASIA-Webface dataset (n = 10575)上训练一个模型，loss将会从9.27降到8.50左右，这个条件下的边界（bound）是8.27，很接近实际值。这表示我们的限制（bound）很紧。为直观认识这个bound，可以看图5。

在这个bound下，收敛问题的解决方法就很清晰了。通过归一化特征和权重矩阵的列到更大的值l，而不是1，这样softmax loss就可以持续下降收敛了。在实际应用中，我们实现这个方法可能会通过在余弦层后添加一个scale层，而这个scale只有一个可训练的参数s=l x l。我们也可能通过填充一个较大的固定值实现，参考图5，如根据类别数设为20或30。然而，我们更倾向于让这个参数可以在反向传播中自动训练获得，而不是引入一个新的超参数。所以最后带有余弦距离的softmax loss定义如下，其中x~是x的归一化结果。

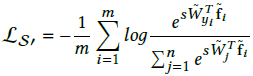
REFORMULATING METRIC LEARNING

度量学习（metric learning），特别是深度度量学习，通常以成对(pairs)或三个样本(triplets)作为输入，然后输出它们的距离。在深度度量模型（deep metric models）中，对特征进行归一化是个很常用的策略。就好像归一化操作对度量学习的损失函数没有造成任何问题一样。然而度量学习的训练比分类的训练要困难一些，因为在度量模型中输入pairs或triplets的样本组合情况非常多，也就是pairs有O(N^2)种组合，triplets有O(N^3)种，其中N是训练样本总数。在训练的时候几乎不可能处理所有的组合情况，因此都会使用一些采样或困难样本挖掘的方法进行训练。相反，对于分类任务，我们通常反复地把数据输入到模型中，即输入数据是O(N)的。所以这里尝试在保留度量学习对归一化特征的兼容性的同时，重新定义（reformulated ）一些度量学习的损失函数去做分类任务。

在人脸验证方面，被广泛应用的度量学习方法有contrastive loss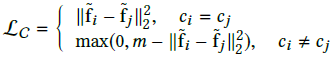：；triplet loss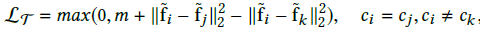：，其中m都是margins。两个损失函数都对特征对间的归一化欧式距离进行了优化。在归一化后，这重新定义的softmax loss也可以被看成是对归一化欧氏距离进行优化：

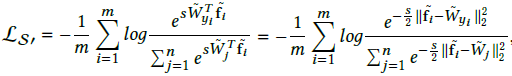
因为，受该公式启发，作者将一个特征作为d x n的权重矩阵W中的一列，d为特征维度，n为类别数，以列Wi作为第i类的“agent”。这权重矩阵W可以作为一个内积层通过反向传播进行训练。这样可以得到分类版本的contrastive loss: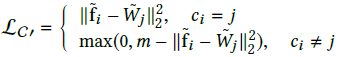和triplet loss：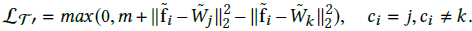

为了将这两个loss函数与度量学习版本的区分开来，这里分别称其C-contrastive loss和C-triplet loss，表示这两个loss都是为分类设计的。直观地，Wj可以看成是特征在第j类上的总结摘要。如果所有类别都可以通过这个margin进行很好的区分，那么Wj则大致相当于各个类别的均值特征（如图6左）。在一些更复杂的任务中，来自不同类别的特征可能会相互重叠，则Wj就会从偏离边界，marginal features（困难样本）就会引导着去获得更大的梯度（如图6右），这意味着它们在更新的时候移动更多。

但这种agent的策略也有一些副作用，在重新定义公式后，如果我们仍然使用原始版本中相同的margin时，一些marginal features可能不会被优化（如图7）。因此我们需要更大的margins来使更多特征得到优化。从数学上将，agent近似所引起的误差是以下命题造成的（推导过程看论文附录7.2）：

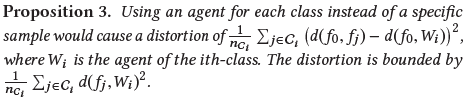
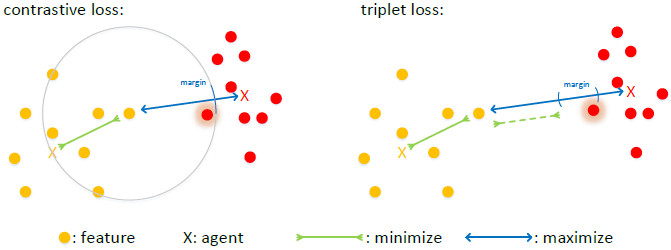
这个假定可以对设置margin起引导作用，从经验得，修改后的contrastive loss和triplet loss的margin分别推荐设为1和0.8。需要注意的是，设置margin通常是一项复杂工作，按以往的算法，需要在每隔训练多个epoch时，将训练挂起去搜索新的margin。然而，这里在归一化后，并不需要这样的搜索算法。通过归一化，特征的量级大小就已经是固定了，这就使margin也可能固定了。则在这个策略下，将不再尝试在没有归一化的情况使用C-contrastive loss或C-triplet loss去训练模型了，因为不归一化时使用这两个loss需要不断迭代搜索新的margin，过程复杂。

REFORMULATING METRIC LEARNING