论文: He K, Zhang X, Ren S, et al. Deep Residual Learning for Image Recognition[J]. Computer Science, 2015.
Github: https://github.com/KaimingHe/deep-residual-networks
译文推荐:http://www.cnfeelings.com/future/53100
论文算法概述
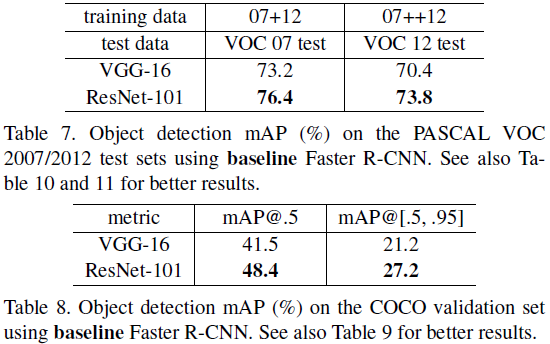
深度网络可以提取到低/中/高层的特征,通过增加网络层数可以丰富提取到的特征。但训练一个好的模型并不是直接叠加更多的网络层就可以实现的。在增加层数时会有梯度弥散和梯度暴增的问题,使网络难以收敛,而normalized initialization [23, 9, 37, 13] and intermediate normalization layers[16]可以很大程度上解决这些问题。但网络逐渐收敛后,还有可能会遇到degradation(退化)问题,即网络加深了,在没有产生过拟合情况下,准确率却下降了。如图1所示,在合适的网络的基础上增加网络层数,而产生了更大的误差。这表明并不是所有网络那么容易优化的。文中提出的深度残差学习框架可以解决degradation问题。
假设我们期望的网络层关系映射为H(x), 我们让 the stacked nonlinear layers 拟合另一个映射,F(x):= H(x)-x,那么原先的映射就是 F(x)+x。 这里我们假设优化残差映射F(x) 比优化原来的映射 H(x)容易。F(x)+x可以通过shortcut connections 来实现,如下图所示:

残差学习
(与训练减均值类似)设H(x)为多个堆叠在一起的网络的期望的关系映射,x为原始输入。假定多个非线性网络可以慢慢逼近复杂函数,那么也就同样可以逼近残差函数H(x)-x(假设输入输出维度相等)。因此我们可以让网络逼近残差函数F(x) := H(x)-x,则原始的函数为F(x)+x。
增加的网络层如果可以被构建为相应的关系映射,则更深层次的网络的训练误差会更小。而degradation问题表明直接通过多个非线性网络层去逼近identity mappings存在一定难度,在进行残差学习时,如果identity mappings是最优的,则会直接将这多个非线性层的权重置0去接近identity mappings。
在实际中,identity mappings不太可能达到最优,但残差学习可以帮助预处理这些问题。如果一个最优的函数相对与zero mappings来说更靠近identity mappings,那么它应该更容易基于identity mappings去学习,而不用重新学习。
Identity Mapping by Shortcuts
在多个堆叠层中采用残差学习,其构件(building block)如图2所示,假定输入x和输出y的维度一致,定义为y = F( x, {Wi} ) + x;若维度不一致,可通过a linear projection Ws去转换维度:y = F( x, {Wi} ) +Ws x。而残差函数F是可变的,可以包含有两个或三个甚至更多网络层。但如果只有一层,那么该building block与一个线性层相类似,即y=W1 x + x。
网络结构
Plain Network提出受VGG启发,主要采用3*3卷积,并且有以下两个规则:1)对于相同输出特征图尺寸,网络层则有相同个数的滤波器;2)如果特征图尺寸缩小一半,滤波器个数加倍以保持每层的计算复杂度。通过步长为2的卷积来进行降采样。总共有34个权重层。 该网络与VGG相比,滤波器要少,复杂度要小。Residual Network则主要是在plain network上加入shortcut connections。

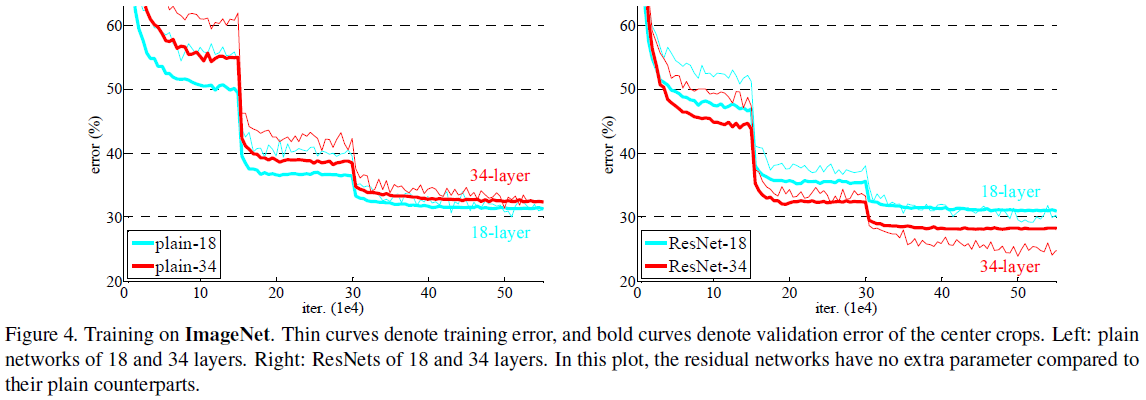
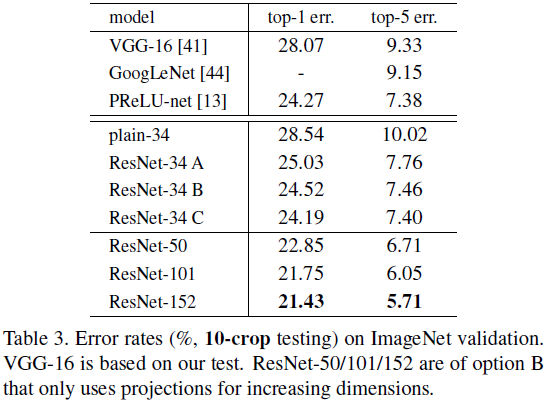
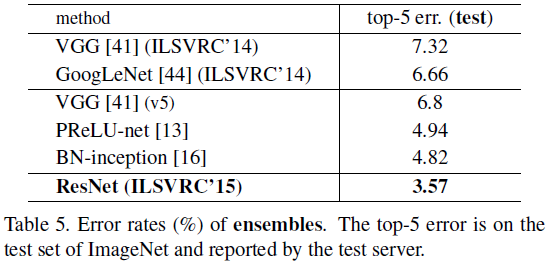
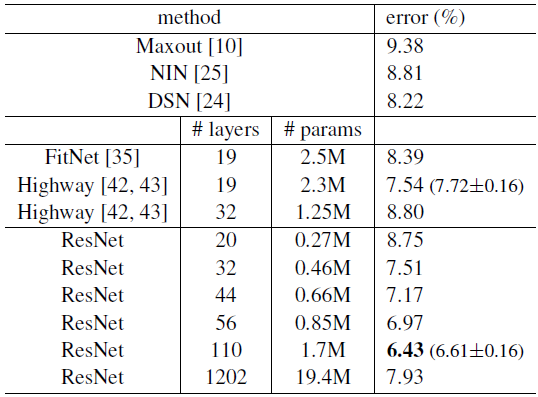
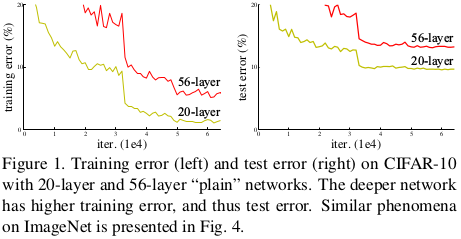
实验测试结果