论文: Wang P, Chen P, Yuan Y, et al. Understanding Convolution for Semantic Segmentation[J]. 2017.
论文算法概述
作者实现了一种dense upsampling convolution(UDC)去得到像素级的预测,可以提取出更多的细节信息,而如果单纯使用双线性插值进行上采样,这些信息通常会被丢失掉;第二是还提出了一种hybrid dilated convolution (HDC)框架应用到编码的阶段中。
该框架有两个优势:1)能高效地扩大网络的感受野,以融合全局信息。2)能减轻由标准的dilated convolution操作造成的网络效应。在多个测试集上达到state-of-the-art。
Dilated Convolution
Dilated Convolution (or Atrous convolution)(进一步可参考论文《Multi-scale Context Aggregation by Dilated Convolutions》)最初设计用于小波分解,主要思想是在卷积核对应像素之间插入空洞来提高图像的分辨率,使能够的深度网络中提取稠密特征。在语义分割框架中,dilated convolution也被用来扩大卷积核的感受野。在其他视觉任务中,dilated convolution也常会被使用到。
Dense Upsampling Convolution (DUC)
设输入图像高宽为H/W,通道数为C,则像素级的语义分割就是生成H x W的标签图,每个像素都有一个类别信息。在输入到一个深度全卷积网络后,在进行预测之前会得到一个h x w x c的特征图,其中h=H/r,w=W/r,r为下采样因子。DUC使用卷积操作直接在特征图上得到逐像素的预测结果,而不像双线性上采样那样参数不可训练,也不像反卷积那样在卷积操作之前的非池化步骤中需要使用0去填充。
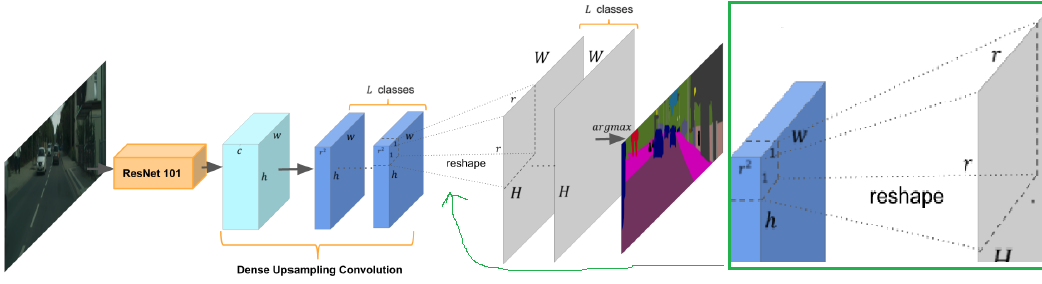
在DUC中,如上图,卷积操作应用在来自ResNet的h x w x c大小的特征图上,以得到h x w x (r x r x L)的输出特征图,其中L是语义分割任务中的类别数。输出特征图上使用softmax层缩放到H x W x L(H=h/r,W=w/r),并利用逐像素取极值的运算去获得最终的标签图。DUC的主要思想是,将整个标签图分成多个相同大小的子块,所有子块都会堆叠r x r次去生成整个标签图。也就是说,将整个标签图转换成有多个通道的更小的标签图,这样的转换使可以在输入特征图和输出标签图之间直接采样卷积操作,而不需要像反卷积层(unpooling操作)那样插入额外的像素。
DUC是可训练的,所以它有能力去提取和恢复在双线性插值上很容易丢失的细粒度信息。例如,一个网络的下采样比率是1/16,而一个物体的长或宽小于16个像素,那么双线性插值将不能把这个下采样后的物体做上采样复原。同时,对应的训练标签也必须要下采样到对应的输出维度,这样会导致细节信息的丢失。
对于DUC的预测结果,对应着原始分辨率,所以支持像素级的解码。另外DUC操作可以很好地应用到FCN框架中,使整个编解码过程是端到端训练的。
Hybrid Dilated Convolution (HDC)
在1D空间上,设f[i]为输入信号,g[i]为输出信号,h[l]表示长度为l的滤波器,r对应用来采样f[i]的dilation rate(在标准卷积中r=1),则dilated convolution公式定义如下:
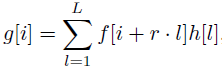
在语义分割系统中,2D的dilated convolution即在卷积核内每个像素之间插入0。对于一个k x k卷积核,对应的dilated滤波器为kd x kd,其中kd = k + (k - 1) x (r - 1)。dilated convolution的作用是保持FCN过程中的特征图分辨率,具体是通过在固定感受野大小的同时替换极大值池化操作或步长大于1的卷积操作来实现。例如,如果在ResNet-101上的一个卷积层的stride s=2,然后将这个步长设为1去掉下采样过程,然后将该层随后的卷积层的所有卷积核的dilation rate r设为2,该过程迭代地应用到所有含有下采样操作的网络层中,因此在输出层的特征图可以保持与输入图像一样的分辨率。而在实践中,dilated convolution通常会应用到已经进行了下采样的特征图上,来达到速度和准确率之间合理的平衡。
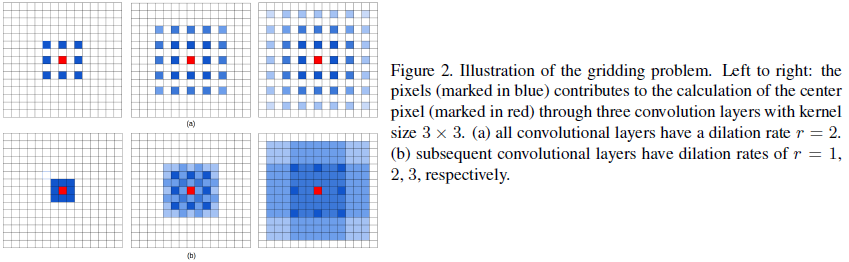
但在上述提到的dilated convolution框架中存在一个问题,称为“gridding”,如图2所示。对于一个在dilated convolution层l上的像素p,其涵盖的信息主要来自第l-1层网络中以p为中心的kd x kd个像素中。而dilated convolution在卷积核中引入了0,则实际参与到计算中的像素则由kd x kd变成了k x k,存在着r-1的间隙在它们之间。如果k=3,r=2,则区域对应25个像素中只有9个像素被用于计算(如图2a)。因为所有层都有相同的dilation rate r,则对于顶层的dilated convolution层l_top上的像素p,对其有贡献的最大可能的像素个数为(w’ x h’)/(r x r), 其中w’和h’为底层dilated convolution层的宽和高。在额外的降采样操作中,r在更高层时会变得更大,输入就变得更加稀疏,这可能并不利于训练。作者认为原因主要有两个:1)局部信息完全丢失了;2)信息跨过较大的距离后变得互不相关;
文中提出了hybrid dilated convolution(HDC)作为上述问题的解决方案,针对每层使用不同的dilation rate,大体呈波浪锯齿的形式。例如,原先的每层的将dilation rate为2,则将3个连续的层看成是一组,将dilation rate分别改成1、2、3,这样顶层可以从较广的范围的像素中获取信息,然后重复至所有层,因此顶层的感受野也没有发生改变。
HDC的另外一个有点是,它在处理中可以使用任意的dilation rates,因此就扩大了网络的感受野,对于识别相对较大的物体有优势。但需要注意的是在同一组的dilation rate不应该有公因数的关系(如2,4,8等),否则栅格效应(gridding effect)在顶层仍然会存在。
Experiments and Results

