论文： Rastegari M, Ordonez V, Redmon J, et al. XNOR-Net: ImageNet Classification Using Binary Convolutional Neural Networks[J]. 2016:525-542.
Github: https://github.com/allenai/XNOR-Net
论文算法概述
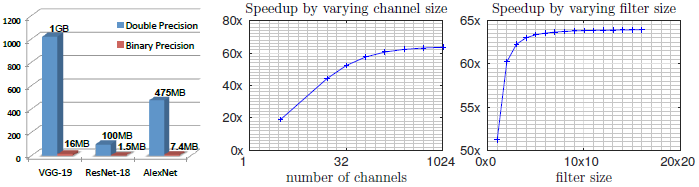
在论文中以加快运算速度为目的，牺牲少许准确率为代价，提出了两个简化网络：Binary-Weight-Networks 和XNOR-Networks。其中Binary-Weight-Networks中，滤波器参数被二值化，节省了32倍的内存空间。在XNOR-Networks中，滤波器和卷积层的输入都被二值化。其中XNOR-Networks的卷积操作以根本上的二值操作进行近似，使其比普通的卷积操作快58倍并节省32倍内存。
压缩权重，也考虑速度。
Binary Convolutional Neural Network
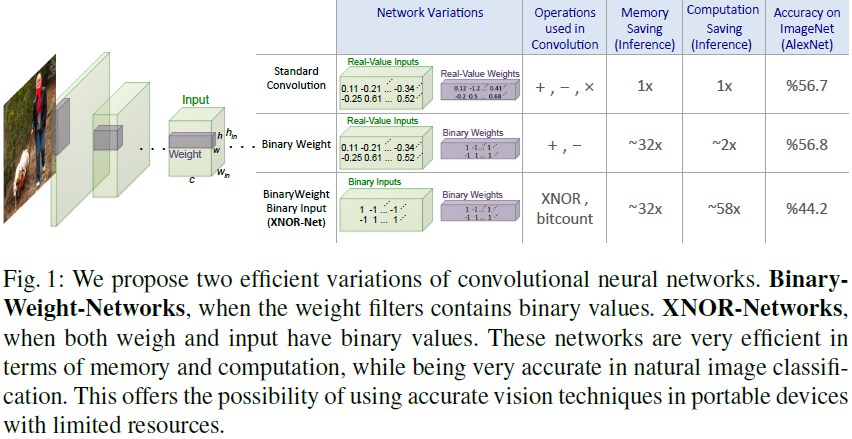
以一个三元组<I_,W_,>表示一个L层的CNN结构，I_为一个张量集，每个元素是CNN网络上对应层的输入张量（如图1中绿色立方体）。W_也是一个张量集，每个元素表示网络中某一层的某个滤波器的权重，表示卷积操作。Binary-weights中W_为二值化张量，XNOR-Networks中I_和W_都是二值化张量。
Binary-Weight-Networks
为约束卷积网络<I_,W_,*>有二值化的权重参数，这里使用（-1，+1）的二值化模板B和一个缩放因子a来估计实数的权重参数，即W约等于aB，一个卷积操作可以近似为：
,其中I和B之间的符号表示没有乘法操作的卷积运算。由于权重是二值化的，所以可以使用加和减来完成卷积运算。这二值化的权重相对于单精度的来说，内存消耗减少了32倍。
Estimating binary weights：没有的广义上的loss，为了给W约等于aB找到一个最佳的估计，解决一下的优化过程：
Training Binary-Weights-Networks：训练CNN过程的每次迭代都涉及前向/反向传播和权重更新三步。在训练带有二值化卷积权重的CNN时，只需要在前向和反向传播过程中将权重进行二值化。为计算sign函数sign(r)的梯度，采用Binarynet论文中提到的方法，即有
，在反向传播中，scaled sign函数的梯度为
。为更新参数，使用高精度（实数）的权重。因为在梯度下降时，参数变化很小，在更新完参数后的二值化会忽略这些改变，影响训练。
下图展示训练带二值化权重的CNN网络的过程。首先，通过计算B和A（上面提到的二值化模板和缩放因子的张量）将每层网络的权重滤波器二值化。然后使用二值化权重和其对应的缩放因子进行前向传播，所有的卷积操作都如公式（1）所示。然后进行反向传播，其中的梯度都由估计的权重滤波器计算得到。最后以一些更新规则（如SGD或ADAM等）更新权重参数。当训练结果后，则不需要保留实数的权重，因为在推断过程中只需要以二值化权重的基础上进行前向传播。
XNOR-Networks
前面的内容中，我们尝试找到二值化权重和缩放因子去近似实数权重，而卷积层的输入仍然是实数的张量。这里开始解释如果把权重和输入都做二值化，这样卷积操作可以通过XNOR和bitcounting来高效的实现。一个卷积包含重复的移动和点积操作，移动操作将权重滤波器在输入中移动，而点积则在权重滤波器和输入的对应部分进行像素级的乘法运算。如果将点积运算用二值化操作来实现，那么卷积就可以被近似为使用二值化操作来实现了。在两个二值化向量之间的点积运算可以用XNOR-Bitcounting（论文BinaryNet中提出）来实现。
Binary Dot Product：
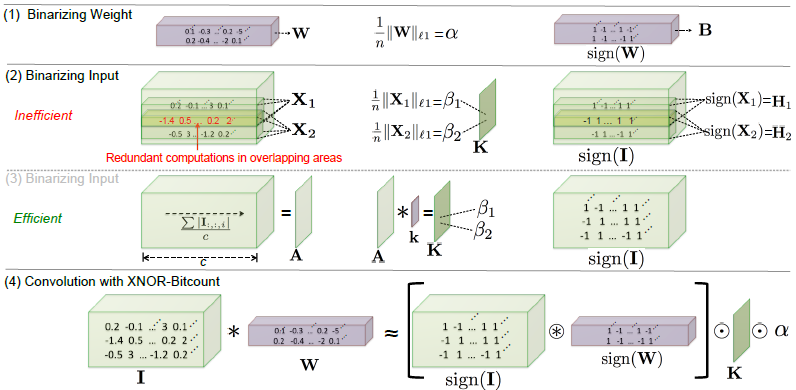
Binary Convolution：卷积滤波器W和输入张量I，需要计算输入张量I中对应W大小的所有可能的子张量的缩放因子beta。其中两个子张量如图2中X1和X2所示。由于子张量之间的重叠，计算所有可能的子张量的beta的计算量很大，为减小这个计算负担，首先需要计算一个矩阵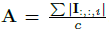
，这是输入I的所有通道元素的绝对值均值，然后用一个2D滤波器k与A卷积，K = A * k，K包含用于I的所有子张量的缩放因子beta，K_ij对应于所有以位置(i,j)为中心的子张量的beta。这个过程如图2第3行所示。当获得W的缩放因子alpha和子张量的缩放因子beta（以K表示）后，可以用以下二值化操作来近似输入I和权重W之间的卷积运算：
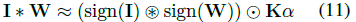。其中圈内加*，表示使用XNOR和bitcount操作的卷积运算。如图2最后一行所示。
Training XNOR-Networks：CNN的一个典型的block包含几个网络层，如图3左所示，该block有4层，1-Convolutional，2-Batch Normalization，3-Activation，4-Pooling。在二值化输入中采用池化操作会导致信息的大量丢失，因此这里将池化操作放到卷积后面。为更大程度上减少二值化导致的信息丢失，作者将输入在进行二值化之前做了归一化，这样保证了数据具有0均值，使以0作为二值化阈值时的量化误差更小。Block的结构如图3右所示。这二值化激活层（BinActiv）计算了K和sign(I)，下一层（BinConv）在给定K和sign(I)的情况下，通过公式(11)计算二值化卷积。然后最后一层进行池化。训练过程与上面的algorithm 1一样。
Binary Gradient：这计算瓶颈在于在每一层的方向传播中计算权重W和输入的梯度(gin)之间的卷积。与前向计算的二值化类似，我们可以将反向传播的gin二值化。这样会是训练过程变得很高效。需要注意的是，如果我们使用公式（6）去计算gin的缩放因子，那么SGD中，最大变幅（maximum change）的方向会被削弱。为在每个维度上保留这最大变化，作者采用
作为缩放因子。
k-bit Quantization:：论文到这里为止，展示的都是采用sign函数的权重和输入的1-bit量化。但也可以使用
代替sign函数，很容易地将量化等级扩展到k-bits，式子中[.]表示取整操作，且x在[-1,1]之间。
Experiments
