论文： Courbariaux M, Bengio Y. BinaryNet: Training Deep Neural Networks with Weights and Activations Constrained to +1 or -1[J]. 2016.
Github：https://github.com/MatthieuCourbariaux/BinaryNet
论文算法概述
BinaryNet的权重和激活值均为二值化值，通过以1bit的异或非（xnor）运算将大多数的乘法运算替换掉，牺牲少许精度使内存消耗大大减少。
压缩权重，也考虑速度。
Sign function
BinaryNet将权重和激活值都限制到-1或+1，而这二值化的函数是简单的sign函数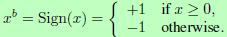
Gradients computation and accumulation
尽管在计算参数梯度时，权重和激活值都是二值化的，但使用了实数变量对权重的实数梯度进行累计，如Algorithm 1所示。实数权重一般会采用SGD进行优化，SGD是一小步一步地去探索参数空间，而每一小步都会含有一些噪声（即每一步的方向都不一定是指向全局最优的方向），而这些噪声可以通过在与权重的每次累加中被均衡化。因此，为这些累加保留足够的分辨率是很重要的。除此之外，在计算梯度时，给权重和激活值添加噪声能起到正则化的作用，提高泛化能力。而BinaryNet 可以看成是Dropout的变体，将激活值和权重进行二值化，而不是在计算梯度时随机把激活值设0。
Propagating Gradients Through Discretization
sign函数的导数几乎都为0，所以不适合直接用于反向传播。考虑到sign函数的量化q=sign(r)，并假定rho C/rho q的估计函数g_q已经被实现了，那么这里rho C/rho q的直连估计函数（straight-through estimator）可以简化为： 。这样保留了梯度信息，而且在r太大时可以取消掉该梯度。该直连估计函数的使用解释如Algorithm 1中所示，1_ |
r | <=1的导数可以看成是通过hard tanh进行梯度传播，遵循着分段线性激活函数Htanh(x) = Clip(x ,-1, 1) = max(-1 , min(1, x))。对于隐藏神经元，使用sign函数的非线性去得到二值化激活值，而对于权重，这里结合了部分：1）约束每个实数权重到-1与1之间，如Algorithm 1所示，否则权重会变得很大；2）使用sign()对实数权重值进行量化。 |
还有其他一些方法也对BinaryNet有利：1）Batch Normalization (BN) ，具体如Algorithm2所示，加速训练过程也减少了整体权重的尺度影响，而归一化噪声也可能有利于规范化模型；2）ADAM训练规则，具体如Algorithm3所示，也似乎有助于减少整体权重的尺度影响；
