概述
对一个函数在空间和时间上进行局部化的一种数学变换。通过平移母小波获得信号的时间信息；通过缩放小波的宽度（或称尺度）获得信号的频率特性；对母小波的平移和缩放操作时为计算小波的系数，这些系数代表局部信号和小波之间的相互性。（关联：多分辨率、图像金字塔）
小波：一个具有震荡性和迅速衰减的波，具有有限区间和均值为零。其中 “小”是指在时域具有紧支集或近似紧支集，“波”是指具有正负交替的波动性，直流分量为0。在数学上满足，同时其频谱：
，满足条件：
。
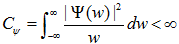小波基函数：通过对基本小波进行尺度上的伸缩和位置上的移动、可形成一系列小波函数—小波基函数，一组小波基函数是通过尺度因子a和位移因子b由基本小波来产生：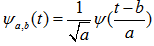 
连续小波变换定义：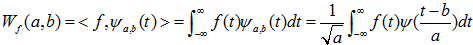 
； 连续小波变换的逆变换： 
；
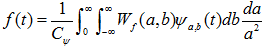小波变换的参数：小尺度–>对应与压缩的小波，可表征更好的细节（变化）：高频率； 大尺度–>对应于展开的小波，表征粗糙部分（慢变化）：低频率。
小波变换的基本性质：
-
线性：小波变换是线性变换，
，
；
-
平移和伸缩的共变性：
； -
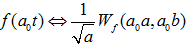冗余性：连续小波变换中存在信息表述的冗余度，如由连续小波变换恢复原信号的重构公式不唯一，小波变换的核函数存在许多可能的选择；
-
尽管冗余的存在可以提高信号重建时计算的稳定性，但增加了分析和解小波变换的结果。
在图像处理中的一般步骤（未使用Mallat算法的一般变换步骤，与gabor小波一样）：
-
把小波w(t)和原函数f(t)的开始部分进行比较，计算系数C。系数C表示该部分函数与小波的相似程度；
-
把小波向右移k单位，得到小波w(t-k)，重复1。重复该部知道函数f结束；
-
扩展小波w(t)，得到小波w(t/2)，重复步骤1,2；
-
不断扩展小波，重复1,2,3.
缺点：
-
应用时小波基的选取较难；
-
存在冗余。
从傅立叶变换到小波变换（对比）：
傅立叶变换：傅立叶变换反映的是图像的整体特征，其频域分析具有很好的局部性，但空间（时间）域上没有局部化功能；傅立叶变换公式为，意味着信号在所有时间区间与复指数相乘，结果产生傅立叶变换F(w)，按照傅立叶系数，可将原信号分解为不同频率的组合。如下图所示。
小波变换：小波变换是空间（时间）和频率的局部变换，它通过伸缩平移运算对信号逐步进行多尺度细化，最终达到高频处时间细分，低频处频率细分，能自动适应时频信号分析的要求，从而可聚焦到信号的任意细节，是基于多分辨率理论的分析基础；小波变换可理解未用经过缩放和平移的一系列函数代替傅立叶变换用的正弦波。变换是结果产生小波变换系数，按照小波系数，原始信号分解为不同小波的组合。如下图所示。小波变换的速度比傅立叶变换快一个数量级。
小波基的选择
小波基的评价指标：正交性、紧支性与衰减性、对称性、正则性、消失矩阶数、线性相位。
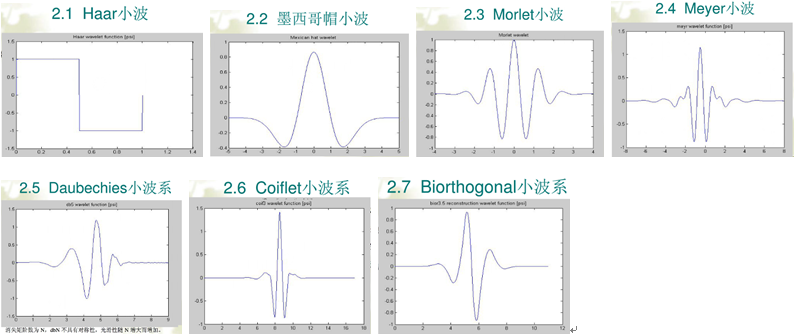
常用的基本小波：
