概述
傅立叶变换的缺点：傅立叶变换是信号在整个时域内的积分，因此傅立叶频谱知识信号频率的统计特性，没有局部化分析信号的功能。
Gabor变换的思想：把信号划分程序多小的时间间隔，用傅立叶变换分析每一个时间间隔一边确定信号在该事件间隔存在的频率。其处理方法是引入了时间局部化的窗函数，对信号施加一个滑动窗口（高斯函数）后，再作傅立叶变换。得到窗口傅里叶变换，又称为短时傅里叶变换STFT。可以在频域不同尺度、不同方向上提取相关的局部方向性特征。
Gabor公式：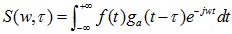 
，其中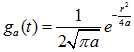
为高斯函数，可以看出：在 Gabor 变换中可以通过控制 来控制窗函数的移动，通过控制a值来控制高斯函数形状，也就是控制时间精度，a越小，其时间窗就越窄。（个人：当a不变时为经典的gabor变换，而a变化的则为gabor小波变换，因为其思想与小波变换一样，看小波变换中“在图像处理中的一般步骤”）。
变换步骤：1）选定一个有限窗口； 2）将窗口放置于信号的起点； 3）计算窗口内信号的傅里叶变换； 4）将窗口向右移动一个小距离； 5）重复3、4步，直至达到信号的末尾。
特征：1）实现了对信号的频率与实践观察的折衷； 2）无论时间还是频率的观察均为有限精度，整体精度取决于窗口的尺寸； 3）一旦窗口尺寸确定，将作用于所有频率。
滑动窗口取高斯函数的原因：一是高斯函数的Fourier变换仍为高斯函数，这使得Fourier逆变换也是用窗函数局部化，同时体现了频域的局部化；二是Gabor变换是最优的窗口Fourier变换。其意义在于Gabor变换出现之后，才有了真正意义上的时间－频率分析。即Gabor变换可以达到时频局部化的目的：它能够在整体上提供信号的全部信息而又能提供在任一局部时间内信号变化剧烈程度的信息。简言之，可以同时提供时域和频域局部化的信息。
二维Gabor滤波器
二维Gabor滤波器，可由一维推得，就变换过程，gabor小波变换就是小波变换，所谓gabor变换和gabor小波变换区别在于其高斯核固定与不固定.
用Gabor 函数形成的二维Gabor 滤波器具有在空间域和频率域同时取得最优局部化的特性，因此能够很好地描述对应于空间频率(尺度)、空间位置及方向选择性的局部结构信息；在空域，一个2维的Gabor滤波器是一个正弦平面波和高斯核函数的乘积。Gabor滤波器是自相似的，也就是说，所有Gabor滤波器都可以从一个母小波经过膨胀和旋转产生。实际应用中，Gabor滤波器可以在频域的不同尺度，不同方向上提取相关特征。其中二维Gabor滤波器g（x，y）公式如下图所示。
从空域来看，Gabor滤波器是高斯核函数调制正弦平面波（同一维，e指数为正弦函数，窗函数为高斯函数，后做积分）；s(x,y)是复杂的正弦函数，相当于载波；w(x,y)是2维高斯函数包迹。（u0,v0）定义了正弦平面波的时域频率，在极坐标中可用f和Θ来表示。a,b 为x和y方向的椭圆高斯的方差，K=1/ab为高斯包迹的参数，r 为角度旋转的下标，Θ为旋转角度，（x0,y0）为函数峰值，也是接受域的中心。
当用作特征检测时，如下第三幅图，通过改变f和Θ生成不同滤波器(小波变换思想，所以这时常称gabor变换为gabor小波变换)，对图像进行检测。
变换步骤（与小波变换一致，也可使用Mallat算法进行快速运算）：
-
把小波w(t)和原函数f(t)的开始部分进行比较，计算系数C。系数C表示该部分函数与小波的相似程度；
-
把小波向右移k单位，得到小波w(t-k)，重复1。重复该部知道函数f结束；
-
扩展小波w(t)，得到小波w(t/2)，重复步骤1,2；
-
不断扩展小波，重复1,2,3.
即“一高斯核扫一遍，调参数得新高斯核，再扫再调再扫”
在my_gabor例子程序中：
-
利用下图3的第一条公式g，通过调节参数f和Θ，得到各种尺度和方向的gabor小波，将各个gabor小波分别与原图像进行卷积，一个小波（分实部和虚部的卷积核）遍历卷积一次，得到最后一幅图的形式。（卷积：因为空域上的卷积等于频域上的相乘，如在空域上做高通滤波）
-
对结果频谱图采样到一定大小，将得到的矩阵的每个值分别减去均值后除以标准差（做归一化），以求得所谓的gabor特征。
如最后一张图，变换结果与傅立叶变换不同，gabor小波变换能明显提取出各个区域的特征，并保留的位置信息（从频谱图的对应的高频位置能找到产生该高频的空域图中位置）
