概述
傅立叶变换可以准确地知道信号中含有哪些频率成分,但不知道这些成分发生的时间、位置,所以适于表现稳态信号特征,而不适于表现非稳态信号。其中稳态信号特是由一系列不随时间改变的频率组成,不需要知道任何频率的开始与停止时间。而非稳态信号具有随时间变化的频率成分,分析中需要知道什么频率在什么时候发生、特定频率发生的位置。
傅立叶变换的局限性:
-
时间信息损失:什么时候特定的时间发生?
-
位置信息损失:傅立叶变换不能确定某一事件的漂移、趋势、突变、起始和结束等;
-
傅立叶变换分析师全局性的分析,难以分析局部信号特征。
其他局限性:
-
对于瞬态信号或高度局部化的信号(例如边缘),由于这些成分并不类似于任何一个傅立叶基函数,它们的变换系数(频谱)不是紧凑的,频谱上呈现出一幅相当混乱的构成;
-
这种情况下,傅立叶变换是通过复杂的安排,以抵消一些正弦波的方式构造出在大部分区间都为零的函数而实现的;
-
对于包含瞬态或局部变化成分的信号,傅里叶变换分析难于得到最佳的表示。
基本性质
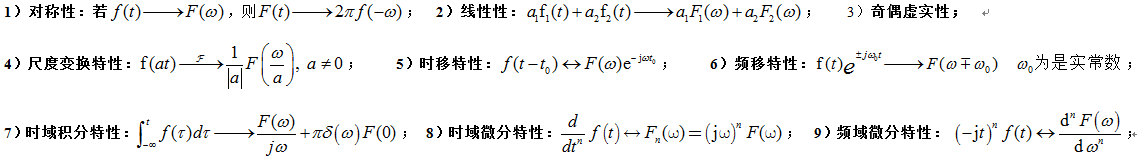
频域的概念、傅立叶变换公式缘由
任何周期函数,都可以看作是不同振幅,不同相位正弦波的叠加。如下图所示,所以傅立叶反变换:,其变量为频率w,即由旋转因子得到旋转方向乘上频率幅度后得到各种正弦波,而一个w频率对应一个旋转因子和幅频的值,做积分将所有的频率的情况都涵盖在内,堆叠起来得到时域函数;而傅立叶变换公式:
“未”,变量为时间t,时域全部幅值分别乘上同一个频率的旋转因子,后叠加,得到该频率的幅度。
功率谱的概念
功率谱表示了信号功率随着频率的变化关系。常用于功率信号(区别于能量信号)的表述与分析,其曲线(即功率谱曲线)一般横坐标为频率,纵坐标为功率。
功率谱:信号先自相关再作FFT; 频谱:信号直接作FFT。
注:高斯函数的傅里叶变换还是高斯函数。

