欧式距离
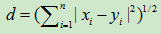
Minkkowsky距离（闵可夫斯基）
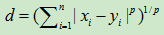
切比雪夫距离
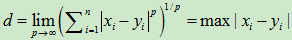
曼哈顿距离
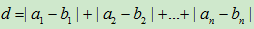
余弦距离测度
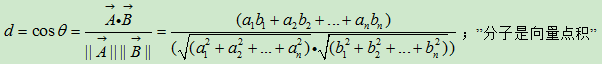
谷本距离测度
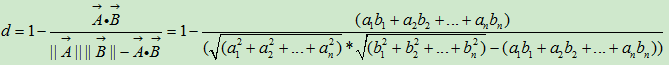
可同时表现点与点之间的夹角和相对距离信息，即在余弦距离的基础上加上相对距离信息。
分析：距离对于坐标系的旋转和位移是不变的，对于放大缩小并不具有不变性的性质。角度相似性函数对于坐标系的旋转、放大和缩小具有不变性，但对于位移不具有不变性的性质。用角度相似性函数作为相似性的测度还有一个缺点，当本属不同类的样本分布在从模式空间原点出发的一条直线上时，所有样本之间角度相似性函数几乎都等于1，造成归一类的错误。
汉明（Hamming）距离
信息论中，汉明距离为两字符串对对应位置不同字符的个数。
马氏距离
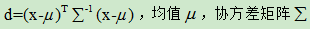
与欧氏距离不同的是它考虑到各种特性之间的联系（例如：一条关于身高的信息会带来一条关于体重的信息，因为两者是有关联的）并且是尺度无关的，即独立于测量尺度。优点：它不受量纲的影响，两点之间的马氏距离与原始数据的测量单位无关；由标准化数据和中心化数据(即原始数据与均值之差）计算出的二点之间的马氏距离相同。马氏距离还可以排除变量之间的相关性的干扰。缺点：它的缺点是夸大了变化微小的变量的作用。
Bhattacharyya距离（巴氏，巴特查里亚）
在统计学中，巴氏距离（巴塔恰里雅距离 / Bhattacharyya distance）用于测量两离散概率分布。它常在分类中测量类之间的可分离性。
在同一定义域X中，概率分布p和q的巴氏距离定义如下：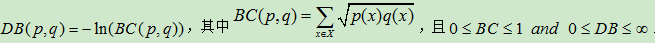
巴氏距离DB均不满足三角不等式。
Hausdorff 豪斯多夫距离（HD）
是描述两组点集之间相似程度的一种度量，即集合之间距离的一种定义形式。若给定两组有限点集合A={a1,a2,…,am} 和B={b1,b2,…,bn}，则Hausdorff 距离定义为H(A,B)=max(h(A,B),h(B,A))， 其中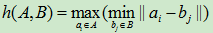
。式中h(A,B)称为集合A 到B的有向Hausdorff 距离，即点集A 中所有点到点集B 的最小距离的最大值。h(B,A)称为反向Hausdorff 距离，它和h(A,B)中的较大着构成点集A 和点集B 的Hausdorff 距离，它度量了两个点集间的最大不匹配程度。图例子：S2中所有的点到点集S1的最小距离如红线所示，其中d2为最大。S1中所有的点到点集S2的最小距离如黑线所示，其中d1为最大。
缺点：易受突发噪声影响。
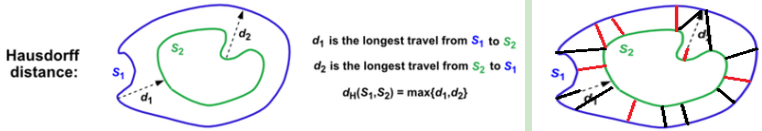
修正的Hausdorff距离（MHD）
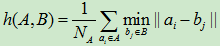
对噪声不太敏感。
Jaccard‘杰卡德’距离
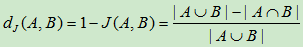
是用来衡量两个集合差异性的一种指标，它是Jaccard相似系数的补集，被定义为1减去Jaccard相似系数。而Jaccard相似系数，也称Jaccard指数，是用来衡量两个集合相似度的一种指标。